「CF498C」Array and Operations
题解
题目显然给出的是二分图
每个质因数分开考虑
将有关的点连inf的边,源向奇点连容量为因子数量的边,偶点向汇连
作最大流
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 |
#include<cstdio> #include<cmath> #include<ctime> #include<cstring> #include<iostream> #include<algorithm> #include<queue> #include<set> #define ll long long #define mod 1000000007 #define inf 1000000000 using namespace std; int read() { int f=1,x=0;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,m,T,cnt,ans; int a[205],u[205],v[205]; int h[205],q[205],last[205],cur[205]; struct edge{ int to,next,v; }e[200005]; void insert(int u,int v,int w) { e[++cnt].to=v;e[cnt].next=last[u];last[u]=cnt;e[cnt].v=w; e[++cnt].to=u;e[cnt].next=last[v];last[v]=cnt;e[cnt].v=0; }; bool bfs() { int head=0,tail=1; for(int i=0;i<=T;i++)h[i]=-1; q[0]=0;h[0]=0; while(head!=tail) { int now=q[head];head++; for(int i=last[now];i;i=e[i].next) if(h[e[i].to]==-1&&e[i].v) { h[e[i].to]=h[now]+1; q[tail++]=e[i].to; } } return h[T]!=-1; } int dfs(int x,int f) { if(x==T)return f; int w,used=0; for(int i=cur[x];i;i=e[i].next) if(h[e[i].to]==h[x]+1) { w=dfs(e[i].to,min(e[i].v,f-used)); e[i].v-=w;e[i^1].v+=w; if(e[i].v)cur[x]=i; used+=w;if(used==f)return f; } if(!used)h[x]=-1; return used; } void dinic() { while(bfs()) { for(int i=0;i<=T;i++) cur[i]=last[i]; ans+=dfs(0,inf); } } void solve(int x) { cnt=1; memset(last,0,sizeof(last)); for(int i=1;i<=n;i++) { int t=0; while(a[i]%x==0)a[i]/=x,t++; if(i&1)insert(0,i,t); else insert(i+n,T,t); } for(int i=1;i<=m;i++) insert(u[i],v[i]+n,inf); dinic(); } int main() { n=read();m=read();T=2*n+1; for(int i=1;i<=n;i++)a[i]=read(); for(int i=1;i<=m;i++) { u[i]=read(),v[i]=read(); if(v[i]&1)swap(u[i],v[i]); } for(int k=1;k<=n;k++) { int t=sqrt(a[k]); for(int i=2;i<=t;i++) if(a[k]%i==0)solve(i); if(a[k]!=1)solve(a[k]); } printf("%d\n",ans); return 0; } |
Subscribe

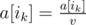 and
and 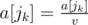 .
.