「CF493E」Vasya and Polynomial
题解
真是神题啊。。。
做了好多英文阅读。。。如有错误请指正。。。
以下默认多项式系数非负
t=a=b=1,有无数解
t=a=b=n(n>1),此时有两解 p(x)=a p(x)=x
以下证明其余情况最多一解
—————————————————————————————-
p(t)=a可以得出多项式的系数和<a,t=1时系数和<=a下面会另外讨论
我们考虑把b在a进制下表示,就能得到一个多项式使得p(a)=b
—–如 1497 = 2 × 93 + 4 ×9 + 3 -> p(x) = 2 x3 + 4 x + 3
由于多项式的系数和<=a,所以我们无法通过调整系数使得存在另一个多项式p'(x)满足p'(a)=b
因为将多项式的任意一个x^k分解
—–如2 x3 + 4 x + 3 -> x3 + 13 x + 3
至少会使得p(x)系数和增加a-1,而p(x)系数和>=1,调整后>=a
(p(x)系数和等于0的情况即a=b,若t<>a=b则显然只有一解p(x)=a)
*但若t=1,且p(x)系数和为1,调整后p'(x)系数和为a,形如p(1)=k,p(k)=k^q,则唯一解为p(x)=k*x^(q-1)
—————————————————————————————-
特判后将b在a进制下表示得到系数后带入t检验即可
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
#include<map> #include<set> #include<cmath> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define ll long long #define mod 1000000007 #define inf 1000000000 using namespace std; ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int h; ll t,a,b; ll f[60]; ll pow(ll x,int y) { ll t=1; for(int i=1;i<=y;i++) t*=x; return t; } void solve(ll t,ll a) { for(int i=h;i;i--) { ll base=pow(t,i); f[i]=a/base; a%=base; } f[0]=a; } int main() { t=read();a=read();b=read(); if(a==b&&b==t) { if(a==1)puts("inf"); else puts("2"); } else if(a==b)puts("1"); else { if(t==1) { h=log(b)/log(a); for(int i=1;i<=h;i++) if(pow(a,i)==b){puts("1");return 0;} } if(a!=1) { h=log(b)/log(a); solve(a,b); ll sum=0; for(int i=0;i<=h;i++) sum+=f[i]*pow(t,i); if(sum!=a)puts("0"); else puts("1"); } else puts("0"); } return 0; } |

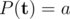 , and
, and  , where
, where  and
and  no greater than
no greater than
楼主,你程序有个bug
1 1 10
这组数据会在 log(b)/log(a) 里面 变成 log(10)/0
恩。。。但是好像不影响结果?
是的,h变成了一个很小的负数,然后没影响结果
不过,有点不好
谢谢你的思路,很有帮助。但是你的程序里h是不需要long long的,换成int就会T了……只能说LL 下溢出的好巧……需要特判一下a = 1的情况。
我加了,但实际上/0在double下是有定义的,是一个inf,用longlong存会溢出为负数