「CF500B」New Year Permutation
User ainta has a permutation p1, p2, …, pn. As the New Year is coming, he wants to make his permutation as pretty as possible.
Permutation a1, a2, …, an is prettier than permutation b1, b2, …, bn, if and only if there exists an integer k (1 ≤ k ≤ n) wherea1 = b1, a2 = b2, …, ak - 1 = bk - 1 and ak < bk all holds.
As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrix A, user ainta can swap the values of pi and pj (1 ≤ i, j ≤ n, i ≠ j) if and only if Ai, j = 1.
Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.
The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.
The second line contains n space-separated integers p1, p2, …, pn — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.
Next n lines describe the matrix A. The i-th line contains n characters ‘0‘ or ‘1‘ and describes the i-th row of A. The j-th character of the i-th line Ai, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, Ai, j = Aj, i holds. Also, for all integers i where 1 ≤ i ≤ n, Ai, i = 0 holds.
In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.
|
1 2 3 4 5 6 7 8 9 |
7 5 2 4 3 6 7 1 0001001 0000000 0000010 1000001 0000000 0010000 1001000 |
|
1 |
1 2 4 3 6 7 5 |
|
1 2 3 4 5 6 7 |
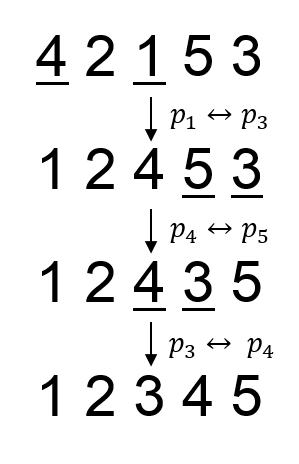
5 4 2 1 5 3 00100 00011 10010 01101 01010 |
|
1 |
1 2 3 4 5 |
In the first sample, the swap needed to obtain the prettiest permutation is: (p1, p7).
In the second sample, the swaps needed to obtain the prettiest permutation is (p1, p3), (p4, p5), (p3, p4).
题解
用并查集维护连通性，从左往右从连通块中每次取出最小的
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<set> #include<ctime> #include<vector> #include<queue> #include<algorithm> #include<map> #include<cmath> #define eps 1e-6 #define inf 1000000000 #define pa pair<int,int> #define ll long long using namespace std; ll read() { ll x=0;char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x; } int n; int p[305],fa[305]; int find(int x) { return x==fa[x]?x:fa[x]=find(fa[x]); } int main() { n=read(); for(int i=1;i<=n;i++)p[i]=read(); for(int i=1;i<=n;i++)fa[i]=i; char ch[305]; for(int i=1;i<=n;i++) { scanf("%s",ch+1); for(int j=1;j<=n;j++) if(ch[j]=='1') { int p=find(i),q=find(j); if(p!=q)fa[p]=q; } } for(int i=1;i<=n;i++) { int t=i; for(int j=i+1;j<=n;j++) if(find(j)==find(i)&&p[j]<p[t])t=j; swap(p[i],p[t]); } for(int i=1;i<=n;i++)printf("%d ",p[i]); return 0; |