「CF500E」New Year Domino
Celebrating the new year, many people post videos of falling dominoes; Here’s a list of them:https://www.youtube.com/results?search_query=New+Years+Dominos
User ainta, who lives in a 2D world, is going to post a video as well.
There are n dominoes on a 2D Cartesian plane. i-th domino (1 ≤ i ≤ n) can be represented as a line segment which is parallel to the y-axis and whose length is li. The lower point of the domino is on the x-axis. Let’s denote the x-coordinate of the i-th domino as pi. Dominoes are placed one after another, so p1 < p2 < … < pn - 1 < pn holds.
User ainta wants to take a video of falling dominoes. To make dominoes fall, he can push a single domino to the right. Then, the domino will fall down drawing a circle-shaped orbit until the line segment totally overlaps with the x-axis.
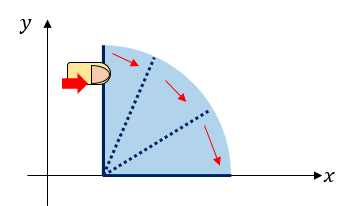
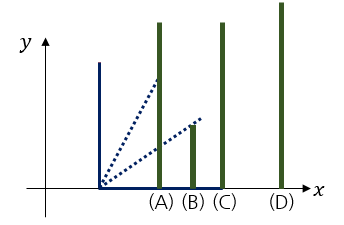
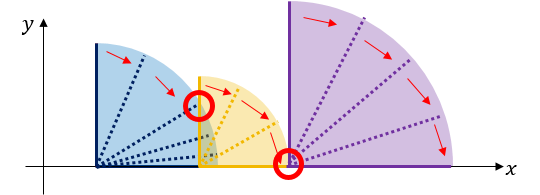
User ainta has q plans of posting the video. j-th of them starts with pushing the xj-th domino, and lasts until the yj-th domino falls. But sometimes, it could be impossible to achieve such plan, so he has to lengthen some dominoes. It costs one dollar to increase the length of a single domino by 1. User ainta wants to know, for each plan, the minimum cost needed to achieve it. Plans are processed independently, i. e. if domino’s length is increased in some plan, it doesn’t affect its length in other plans. Set of dominos that will fall except xj-th domino and yj-th domino doesn’t matter, but the initial push should be on domino xj.
The first line contains an integer n (2 ≤ n ≤ 2 × 105)— the number of dominoes.
Next n lines describe the dominoes. The i-th line (1 ≤ i ≤ n) contains two space-separated integers pi, li (1 ≤ pi, li ≤ 109)— the x-coordinate and the length of the i-th domino. It is guaranteed that p1 < p2 < … < pn - 1 < pn.
The next line contains an integer q (1 ≤ q ≤ 2 × 105) — the number of plans.
Next q lines describe the plans. The j-th line (1 ≤ j ≤ q) contains two space-separated integers xj, yj (1 ≤ xj < yj ≤ n). It means the j-th plan is, to push the xj-th domino, and shoot a video until the yj-th domino falls.
For each plan, print a line containing the minimum cost needed to achieve it. If no cost is needed, print 0.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
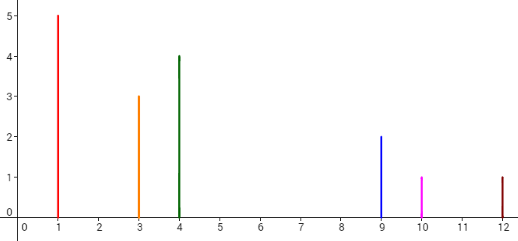
6 1 5 3 3 4 4 9 2 10 1 12 1 4 1 2 2 4 2 5 2 6 |
|
1 2 3 4 |
0 1 1 2 |
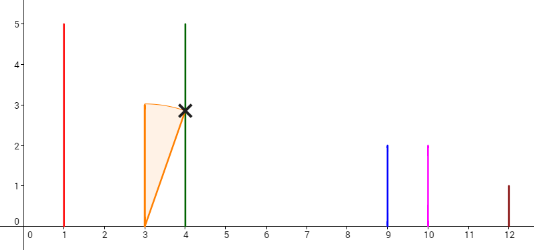
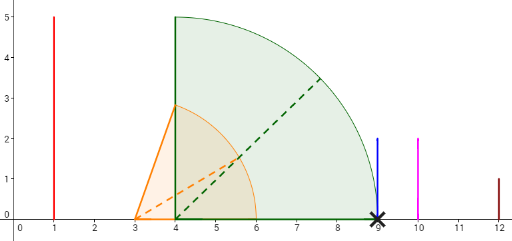
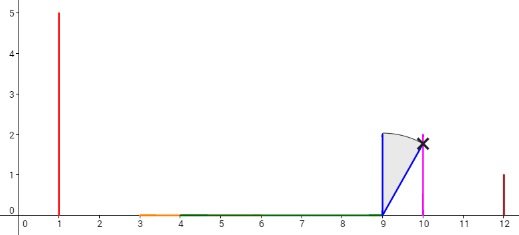
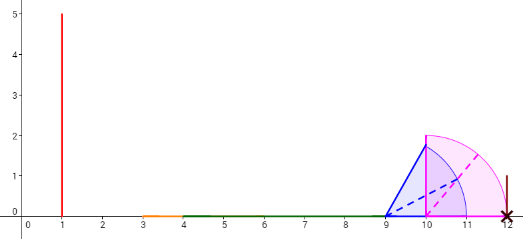
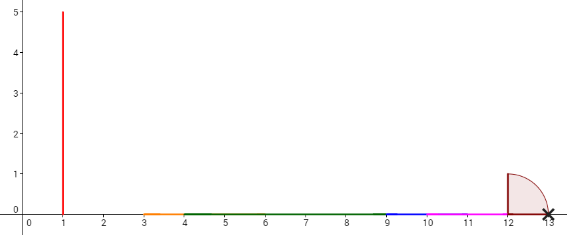
Consider the example. The dominoes are set like the picture below.
这题等于是求一段区间内有多少长度没被覆盖
把多米诺骨牌看成区间,按照倒序处理每个区间,看成是每次这个区间与后面的一些区间并成连通块,处理x为当前区间的查询,这需要知道y属于哪个连通块,用栈+并查集维护,然后再维护一个未覆盖长度的后缀和,就可以O1来回答询问,并成连通块的时候顺便更新这个后缀和。。。额我手残写了什么deque
数组开小了也会wa7。。。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<set> #include<iomanip> #include<ctime> #include<vector> #include<queue> #include<algorithm> #include<map> #include<cmath> #define eps 1e-6 #define inf 1000000000 #define pa pair<int,int> #define ll long long using namespace std; ll read() { ll x=0;char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x; } int n,m; struct data{ int l,r,id; }a[200005]; vector<int> b[200005]; deque<int> q; int l[200005],r[200005]; ll sum[200005],ans[200005]; int x[200005],y[200005],fa[200005],pos[200005]; int find(int x) { return x==fa[x]?x:fa[x]=find(fa[x]); } void solve(int x,int id) { int tmp=y[id]; ans[id]=sum[x]-sum[find(tmp)]; } int main() { n=read(); for(int i=1;i<=n;i++)fa[i]=i; for(int i=1;i<=n;i++) a[i].l=read(),a[i].r=a[i].l+read(); m=read(); for(int i=1;i<=m;i++) { x[i]=read();y[i]=read(); b[x[i]].push_back(i); } for(int i=n;i;i--) { l[i]=a[i].l,r[i]=a[i].r; while(!q.empty()&&l[q.front()]<=r[i]) { r[i]=max(r[i],r[q.front()]); fa[find(q.front())]=i; q.pop_front(); } if(!q.empty())sum[i]=sum[q.front()]+l[q.front()]-r[i]; else sum[i]=0; q.push_front(i); for(int j=0;j<b[i].size();j++) solve(i,b[i][j]); } for(int i=1;i<=m;i++) cout<<ans[i]<<endl; return 0; } |
