「CF444A」DZY Loves Physics
DZY loves Physics, and he enjoys calculating density.
Almost everything has density, even a graph. We define the density of a non-directed graph (nodes and edges of the graph have some values) as follows:
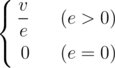
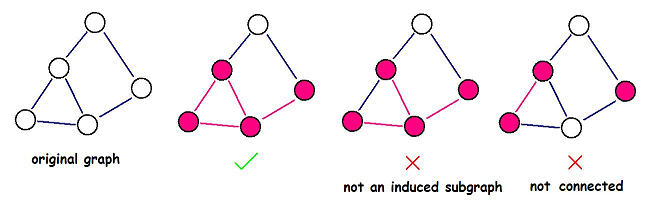
An induced subgraph G‘(V‘, E‘) of a graph G(V, E) is a graph that satisfies:
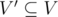;- edge
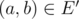if and only if 
, and edge 
; - the value of an edge in G‘ is the same as the value of the corresponding edge in G, so as the value of a node.
Help DZY to find the induced subgraph with maximum density. Note that the induced subgraph you choose must be connected.
The first line contains two space-separated integers n (1 ≤ n ≤ 500),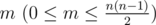 
. Integer n represents the number of nodes of the graph G, m represents the number of edges.
The second line contains n space-separated integers xi (1 ≤ xi ≤ 106), where xi represents the value of the i-th node. Consider the graph nodes are numbered from 1 to n.
Each of the next m lines contains three space-separated integers ai, bi, ci (1 ≤ ai < bi ≤ n; 1 ≤ ci ≤ 103), denoting an edge between node ai and bi with value ci. The graph won’t contain multiple edges.
Output a real number denoting the answer, with an absolute or relative error of at most 10 - 9.
|
1 2 |
1 0 1 |
|
1 |
0.000000000000000 |
|
1 2 3 |
2 1 1 2 1 2 1 |
|
1 |
3.000000000000000 |
|
1 2 3 4 5 6 7 8 |
5 6 13 56 73 98 17 1 2 56 1 3 29 1 4 42 2 3 95 2 4 88 3 4 63 |
|
1 |
2.965517241379311 |
In the first sample, you can only choose an empty subgraph, or the subgraph containing only node 1.
In the second sample, choosing the whole graph is optimal.
题解
可以发现最优解一定只选取了一条边。。。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cstring> #include<cmath> #define inf 0x7fffffff #define ll long long using namespace std; inline ll read() { ll x=0,f=1;char ch=getchar(); while(ch>'9'||ch<'0'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,m; int v[505]; int main() { n=read();m=read(); double ans=0; for(int i=1;i<=n;i++) v[i]=read(); for(int i=1;i<=m;i++) { int a=read(),b=read(),c=read(); ans=max(ans,double(v[a]+v[b])/c); } printf("%.10f",ans); return 0; } |
OI 课件=>
