「BZOJ3275」Number
Description
有N个正整数，需要从中选出一些数，使这些数的和最大。
若两个数a,b同时满足以下条件，则a,b不能同时被选
1:存在正整数C，使a*a+b*b=c*c
2:gcd(a,b)=1
Input
第一行一个正整数n，表示数的个数。
第二行n个正整数a1,a2,?an。
Output
最大的和。
Sample Input
5
3 4 5 6 7
3 4 5 6 7
Sample Output
22
HINT
n<=3000。
题解
将所有点拆成2个
0向i连权为a[i]的边，a[i]向T连权为a[i]的边
有关系的点互相连边，权为inf
答案是tot-ans/2
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
#include<iostream> #include<cstdio> #include<cstring> #include<cmath> #define T 6001 #define inf 0x7fffffff using namespace std; int n,cnt=1,ans,tot; int a[3001],q[6005],h[6005],head[6005],cur[6005]; struct data{int to,next,v;}e[500001]; int gcd(int a,int b){return b==0?a:gcd(b,a%b);} bool jud(int a,int b) { int s=a*a+b*b,q=int(sqrt(s)); if(q*q!=s)return 0; if(gcd(a,b)!=1)return 0; return 1; } void ins(int u,int v,int w) {e[++cnt].to=v;e[cnt].next=head[u];e[cnt].v=w;head[u]=cnt;} void insert(int u,int v,int w) {ins(u,v,w);ins(v,u,0);} bool bfs() { int t=0,w=1; for(int i=0;i<=T;i++)h[i]=-1; q[0]=0;h[0]=0; while(t!=w) { int now=q[t];t++;if(t==6005)t=0; for(int i=head[now];i;i=e[i].next) if(e[i].v&&h[e[i].to]==-1) { h[e[i].to]=h[now]+1; q[w++]=e[i].to;if(w==6005)w=0; } } if(h[T]==-1)return 0; return 1; } int dfs(int x,int f) { if(x==T)return f; int w,used=0; for(int i=cur[x];i;i=e[i].next) { if(e[i].v&&h[e[i].to]==h[x]+1) { w=f-used; w=dfs(e[i].to,min(e[i].v,w)); e[i].v-=w; if(e[i].v)cur[x]=i; e[i^1].v+=w; used+=w;if(used==f)return f; } } if(!used)h[x]=-1; return used; } void dinic() {while(bfs()){for(int i=0;i<=T;i++)cur[i]=head[i];ans+=dfs(0,inf);}} int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); insert(0,i,a[i]); insert(i+n,T,a[i]); tot+=a[i]; } for(int i=1;i<=n;i++) for(int j=i+1;j<=n;j++) if(jud(a[i],a[j])) {insert(i,j+n,inf);insert(j,i+n,inf);} dinic(); printf("%d",tot-ans/2); return 0; } |
计数器 9855207
OI 课件=>
OI 课件=>
题解认真点写行不——看看人家云神写的
为奇数，则从源连一条容量为a 
边到i；
为偶数，则从i连一条容量为a 
的边到汇；
,a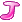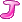 
互斥，则从奇数点连一条容量为无穷大的边到偶数点，
的和减去最大流既是答案。
将数分为两部分，
若a
若a
若a
然后做最大流，a
啊我似乎没分奇偶啊。。
那个……不分奇偶也是可以的，但是似乎可以证明奇数和奇数，偶数和偶数之间似乎是不行的……然后就可以少一半的点
恩
。。。