「CF486D」Valid Sets

2014年11月12日3,1660

As you know, an undirected connected graph with n nodes and n - 1 edges is called a tree. You are given an integer d and a tree consisting of n nodes. Each node i has a value ai associated with it.

We call a set S of tree nodes valid if following conditions are satisfied:

  1. S is non-empty.
  2. S is connected. In other words, if nodes u and v are in S, then all nodes lying on the simple path between u and v should also be presented in S.
  3. .

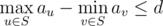Your task is to count the number of valid sets. Since the result can be very large, you must print its remainder modulo1000000007 (109 + 7).

Input

The first line contains two space-separated integers d (0 ≤ d ≤ 2000) and n (1 ≤ n ≤ 2000).

The second line contains n space-separated positive integers a1, a2, …, an(1 ≤ ai ≤ 2000).

Then the next n - 1 line each contain pair of integers u and v (1 ≤ u, v ≤ n) denoting that there is an edge between u and v. It is guaranteed that these edges form a tree.

Output

Print the number of valid sets modulo 1000000007.

Sample test(s)
input

output

input

output

input

output

Note

In the first sample, there are exactly 8 valid sets: {1}, {2}, {3}, {4}, {1, 2}, {1, 3}, {3, 4} and {1, 3, 4}. Set {1, 2, 3, 4}is not valid, because the third condition isn’t satisfied. Set {1, 4} satisfies the third condition, but conflicts with the second condition.

枚举点权的下界，然后直接树形dp

 

avatar
  Subscribe  
提醒