Consider a tree T with N (1 <= N <= 20,000) nodes numbered 1…N. Deleting any node from the tree yields a forest: a collection of one or more trees. Define the balance of a node to be the size of the largest tree in the forest T created by deleting that node from T.
For example, consider the tree:

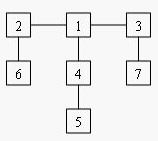
Deleting node 4 yields two trees whose member nodes are {5} and {1,2,3,6,7}. The larger of these two trees has five nodes, thus the balance of node 4 is five. Deleting node 1 yields a forest of three trees of equal size: {2,6}, {3,7}, and {4,5}. Each of these trees has two nodes, so the balance of node 1 is two.For each input tree, calculate the node that has the minimum balance. If multiple nodes have equal balance, output the one with the lowest number.

The first line of input contains a single integer t (1 <= t <= 20), the number of test cases. The first line of each test case contains an integer N (1 <= N <= 20,000), the number of congruence. The next N-1 lines each contains two space-separated node numbers that are the endpoints of an edge in the tree. No edge will be listed twice, and all edges will be listed.

For each test case, print a line containing two integers, the number of the node with minimum balance and the balance of that node.