广度搜索学习总结
BFS,其英文全称是Breadth First Search。 BFS并不使用经验法则算法。从算法的观点,所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。
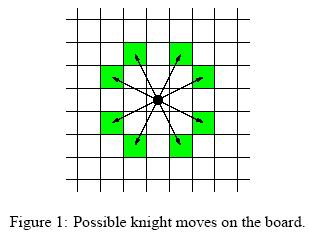
knight moves(本题是最裸的版本)
Background
Mr Somurolov, fabulous chess-gamer indeed, asserts that no one else but him can move knights from one position to another so fast. Can you beat him?
The Problem
Your task is to write a program to calculate the minimum number of moves needed for a knight to reach one point from another, so that you have the chance to be faster than Somurolov.
For people not familiar with chess, the possible knight moves are shown in Figure 1.
输入
The input begins with the number n of scenarios on a single line by itself.
Next follow n scenarios. Each scenario consists of three lines containing integer numbers. The first linespecifies the length l of a side of the chess board (4 <= l <= 300). The entire board has size l * l. Thesecond and third line contain pair of integers {0, …, l-1}*{0, …, l-1} specifying the starting and ending position of the knight on the board. The integers are separated by a single blank. You can assume that the positions are valid positions on the chess board of that scenario.
输出
For each scenario of the input you have to calculate the minimal amount of knight moves which arenecessary to move from the starting point to the ending point. If starting point and ending point areequal,distance is zero. The distance must be written on a single line.
样例输入
样例输出
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
#include<iostream> #include<cstring> using namespace std; int a[300][300]; int xx[8]={1,2,2,1,-1,-2,-2,-1}; int yy[8]={-2,-1,1,2,2,1,-1,-2}; int ox,oy,s; struct data {int x,y,p;} f[50000]; int pd(int x,int y) { if(x>=0&&y>=0&&x<s&&y<s&&a[x][y]==0) return 1; else return 0; } int ans(int x,int y) { if(x==ox&&y==oy) return 1; else return 0; } void search() { memset(a,0,sizeof(a)); int x,y,t=1,w=1; cin>>s>>x>>y>>ox>>oy; a[x][y]=1; f[t].x=x;f[t].y=y;f[t].p=0; if(ans(x,y)){cout<<f[w].p;return;} while(t<=w) { for(int i=0;i<8;i++) { x=f[t].x+xx[i]; y=f[t].y+yy[i]; if(pd(x,y)) { a[x][y]=1; w++; f[w].x=x; f[w].y=y; f[w].p=f[t].p+1; } if(ans(x,y)){cout<<f[w].p<<endl;return;} } t++; } } int main() { int n; cin>>n; for(int i=1;i<=n;i++) { search(); } return 0; } |
紧急救援(在地图中加入了障碍)
题目描述
话说2007年8月5日,Mike博士神秘失踪了,最后发现是被外星人绑架了,幸好外星人目前还是在地球上活动,并且知道外星人不了解地球,幸好,Milk博士身上有无线信号发送装置,我们终于确定了他的位置,必须赶快到那里去救他。
根据无线信号发送装置,我们确定出一张地图,为了尽快寻找到Mike博士,于是这个光荣和艰巨的任务便交给了你,编写程序,通过使用一张地图帮助研究所确定从研究所出发找到Mike博士最短距离。
数据范围: n<=1000
0100110100
0001110010
1000000001
1000100011
0000101100
1000001100
1001010011
0000010100
0101010000
1001000001
1 7
10 2样例输出14
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
#include <iostream> #include <cstring> #include <cstdio> using namespace std; int n; int a[1001][1001]; int xp[4]={0,0,-1,1}, yp[4]={1,-1,0,0}; int xx,yy; struct data{ int x,y,step; }dl[1000000];//队列 int pr(int x,int y)//判断是否为答案 { if(x==xx&&y==yy)return 1; else return 0; } int pd(int x,int y)//用来判断将要搜素的这个点是否可以走 { if(x>=1&&y>=1&&x<=n&&y<=n&&a[x][y]==0) return 1; else return 0; } void bfs() { int x,y,t=1,w=1; cin>>x>>y>>xx>>yy; a[x][y]=1; dl[t].x=x;dl[t].y=y;dl[t].step=0; if(pr(x,y)) {cout<<dl[t].step<<endl;return;} while(t<=w) { for(int i=0;i<4;i++)//搜索周围四个点 {x=dl[t].x+xp[i];y=dl[t].y+yp[i]; if(pd(x,y)) { a[x][y]=1; w++; dl[w].x=x;dl[w].y=y;dl[w].step=dl[t].step+1;//入队 if(pr(x,y)){cout<<dl[w].step<<endl; return;} } } t++; } } int main() { cin>>n; char s[1001]; for(int i=1;i<=n;i++) { scanf("%s",s); for(int j=0;j<n;j++) a[i][j+1]=s[j]-'0'; } bfs(); return 0; } |
武士风度的牛(本题是上两题的结合)
题目描述
这头神奇的牛像其它牛一样喜欢吃草,给你一张地图,上面标注了The Knight的开始位置,树、灌木、石头以及其它障碍的位置,除此之外还有一捆草。现在你的任务是,确定The Knight要想吃到草,至少需要跳多少次。The Knight的位置用’K’来标记,障碍的位置用’*’来标记,草的位置用’H’来标记。
这里有一个地图的例子:
11 | . . . . . . . . . .
10 | . . . . * . . . . .
9 | . . . . . . . . . .
8 | . . . * . * . . . .
7 | . . . . . . . * . .
6 | . . * . . * . . . H
5 | * . . . . . . . . .
4 | . . . * . . . * . .
3 | . K . . . . . . . .
2 | . . . * . . . . . *
1 | . . * . . . . * . .
0 ———————-
1
0 1 2 3 4 5 6 7 8 9 0
The Knight 可以按照下图中的A,B,C,D…这条路径用5次跳到草的地方(有可能其它路线的长度也是5):
11 | . . . . . . . . . .
10 | . . . . * . . . . .
9 | . . . . . . . . . .
8 | . . . * . * . . . .
7 | . . . . . . . * . .
6 | . . * . . * . . . F<
5 | * . B . . . . . . .
4 | . . . * C . . * E .
3 | .>A . . . . D . . .
2 | . . . * . . . . . *
1 | . . * . . . . * . .
0 ———————-
1
0 1 2 3 4 5 6 7 8 9 0
输入
第一行: 两个数,表示农场的列数(< =150)和行数(< =150) 第二行..结尾: 如题目描述的图。
输出
一个数,表示跳跃的最小次数。
样例输入
10 11
……….
….*…..
……….
…*.*….
…….*..
..*..*…H
*………
…*…*..
.K……..
…*…..*
..*….*..
样例输出
5
提示
Hint:这类问题可以用一个简单的先进先出表(队列)来解决。
代码
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 |
#include<iostream> using namespace std; struct data{ int x,y,step; }dl[30000]; int m,n; int bi,bj,ei,ej,t=0,w=1; bool mp[151][151]; int xx[8]={1,1,-1,-1,2,-2,2,-2},yy[8]={2,-2,2,-2,1,1,-1,-1}; bool pd(int i,int j) { if(!mp[i][j]&&i>0&&j>0&&i<=m&&j<=n)return 1; return 0; } void bfs() { if(bi==ei&&bj==ej){cout<<dl[t].step;return;} dl[t].x=bi;dl[t].y=bj;dl[t].step=0; while(t<w) { for(int i=0;i<8;i++) { int x=dl[t].x+xx[i]; int y=dl[t].y+yy[i]; if(pd(x,y)) { mp[x][y]=1; dl[w].x=x; dl[w].y=y; dl[w].step=dl[t].step+1; if(dl[w].x==ei&&dl[w].y==ej){cout<<dl[w].step;return;} w++; } } t++; } } int main() { cin>>n>>m; for(int i=1;i<=m;i++) for(int j=1;j<=n;j++) { char x; cin>>x; if(x=='*')mp[i][j]=1; if(x=='K'){bi=i;bj=j;} if(x=='H'){ei=i;ej=j;} } bfs(); return 0; } |
这类的广搜中还有可能加入传送门等,不过大致来说是一样的
再来一道经典的问题
倒酒问题
题目描述
分别输入三个杯子容量a,b,c 且第一个为初始杯中的酒量,另外两个为空的。现要求你要精确量出
的e容量的酒。问最少通过几步能精确量出你所要的容量。.例如有三个烧杯容量分别为:80、50、30毫升,现在第一个杯中装满了80
毫升水,其余两个是空的。现要精确的40毫升水,不许用其它工具,请找出最少步骤的方法。 若超过100步,则认为这种计量方法太麻烦
,直接输出“no answer”
样例输入
80 50 30 40
样例输出
step1:30 50 0
step2:30 20 30
step3:60 20 0
step4:60 0 20
step5:10 50 20
step6:10 40 30
分析
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 |
#include<iostream> using namespace std; int n,t=0,w=1,m,ans=0; int d[10000][4],f[10000],h[100]; int a,b,c,e; bool pd(int x,int y,int z,int t)//用于判断上层是否已经有这种情况 { for(int k=0;k<w;k++) { if(d[k][0]==t) if(d[k][1]==x&&d[k][2]==y&&d[k][3]==z) return 0; else continue; } return 1; } void an() { if(d[w][1]==e||d[w][2]==e||d[w][3]==e) { ans=1; int s=w; while(s!=0) { h[d[s][0]]=s; s=f[s]; } for(int i=1;i<=d[w][0];i++) { cout<<"step"<<i<<':'<<d[h[i]][1]<<' '<<d[h[i]][2]<<' '<<d[h[i]][3]<<endl; } } } void search() { d[0][1]=a;d[0][2]=0;d[0][3]=0;d[0][0]=0; while(t<w) { if(ans==1||t>100)return; m=min(d[t][1],b-d[t][2]);if(pd(d[t][1]-m,d[t][2]+m,d[t][3],d[t][0])) {f[++w]=t;d[w][1]=d[t][1]-m; d[w][2]=d[t][2]+m;d[w][3]=d[t][3];d[w][0]=d[t][0]+1;an();}//1>2 m=min(d[t][1],c-d[t][3]);if(pd(d[t][1]-m,d[t][2],d[t][3]+m,d[t][0])) {f[++w]=t;d[w][1]=d[t][1]-m; d[w][2]=d[t][2];d[w][3]=d[t][3]+m;d[w][0]=d[t][0]+1;an();}//1>3 m=min(d[t][2],c-d[t][3]);if(pd(d[t][1],d[t][2]-m,d[t][3]+m,d[t][0])) {f[++w]=t;d[w][1]=d[t][1]; d[w][2]=d[t][2]-m;d[w][3]=d[t][3]+m;d[w][0]=d[t][0]+1;an();}//2>3 m=min(d[t][2],a-d[t][1]);if(pd(d[t][1]+m,d[t][2]-m,d[t][3],d[t][0])) {f[++w]=t;d[w][1]=d[t][1]+m; d[w][2]=d[t][2]-m;d[w][3]=d[t][3];d[w][0]=d[t][0]+1;an();}//2>1 m=min(d[t][3],a-d[t][1]);if(pd(d[t][1]+m,d[t][2],d[t][3]-m,d[t][0])) {f[++w]=t;d[w][1]=d[t][1]+m; d[w][2]=d[t][2];d[w][3]=d[t][3]-m;d[w][0]=d[t][0]+1;an();}//3>1 m=min(d[t][3],b-d[t][2]);if(pd(d[t][1],d[t][2]+m,d[t][3]-m,d[t][0])) {f[++w]=t;d[w][1]=d[t][1]; d[w][2]=d[t][2]+m;d[w][3]=d[t][3]-m;d[w][0]=d[t][0]+1;an();}//3>2,??????????? t++; } } int main() { cin>>a>>b>>c>>e; search(); if(ans==0)cout<<"no answer"; return 0; } |
