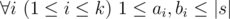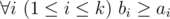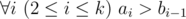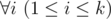「CF494B」Obsessive String
题解
kmp预处理匹配点。。。
f[i]表示前i个的合法划分数。。
f[i]=f[i–1] (表示将最后一个舍弃)
sum[i]=∑ f[k] (k<=i)
设上一个匹配点为last
f[i]+=sum[last–1]+last
即有两种情况
[1….L-1(这部分任意,只要合法,允许舍弃末尾)] [L…i] 这样划分
或者直接 k=1 即只有一个划分[L…i]
L<=last
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
#include<iostream> #include<cstdio> #include<cstdlib> #include<algorithm> #include<cmath> #include<cstring> #define inf 2000000000 #define ll long long #define mod 1000000007 using namespace std; inline int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int top; int fail[100005],q[100005]; char t[100005],s[100005]; ll ans; ll f[100005],sum[100005]; bool mark[100005]; int main() { scanf("%s",t+1); scanf("%s",s+1); int l1=strlen(t+1),l2=strlen(s+1); int k=0; for(int i=2;i<=l2;i++) { while(k>0&&s[k+1]!=s[i])k=fail[k]; if(s[k+1]==s[i])k++; fail[i]=k; } k=0; for(int i=1;i<=l1;i++) { while(k>0&&s[k+1]!=t[i])k=fail[k]; if(s[k+1]==t[i])k++; if(k==l2)k=fail[k],mark[i]=1; } int last=-1; for(int i=1;i<=l1;i++) { f[i]=f[i-1]; if(mark[i])last=i-l2+1; if(last!=-1)f[i]+=sum[last-1]+last; sum[i]=sum[i-1]+f[i]; f[i]%=mod;sum[i]%=mod; } printf("%lld",f[l1]); return 0; } |
Subscribe