「CF415D」Mashmokh and ACM
Mashmokh’s boss, Bimokh, didn’t like Mashmokh. So he fired him. Mashmokh decided to go to university and participate in ACM instead of finding a new job. He wants to become a member of Bamokh’s team. In order to join he was given some programming tasks and one week to solve them. Mashmokh is not a very experienced programmer. Actually he is not a programmer at all. So he wasn’t able to solve them. That’s why he asked you to help him with these tasks. One of these tasks is the following.
A sequence of l integers b1, b2, …, bl (1 ≤ b1 ≤ b2 ≤ … ≤ bl ≤ n) is called good if each number divides (without a remainder) by the next number in the sequence. More formally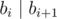 
for all i (1 ≤ i ≤ l - 1).
Given n and k find the number of good sequences of length k. As the answer can be rather large print it modulo 1000000007(109 + 7).
The first line of input contains two space-separated integers n, k (1 ≤ n, k ≤ 2000).
Output a single integer — the number of good sequences of length k modulo 1000000007 (109 + 7).
|
1 |
3 2 |
|
1 |
5 |
|
1 |
6 4 |
|
1 |
39 |
|
1 |
2 1 |
|
1 |
2 |
In the first sample the good sequences are: [1, 1], [2, 2], [3, 3], [1, 2], [1, 3].
题解
很容易想到n^3的dp
然后利用筛法将其变为n^2logn的就行了
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
#include<iostream> #include<cstdio> #define ll long long #define mod 1000000007 using namespace std; int n,m; ll ans,f[2001][2001]; int main() { scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)f[1][i]=1; for(int i=2;i<=m;i++) for(int j=1;j<=n;j++) for(int k=1;k*j<=n;k++) { f[i][j]+=f[i-1][k*j]; f[i][j]%=mod; } for(int i=1;i<=n;i++){ans+=f[m][i];ans%=mod;} printf("%d",ans); return 0; } |
OI 课件=>
