「BZOJ2510」弱题

2014年6月6日4,8006

Description

有M个球，一开始每个球均有一个初始标号，标号范围为1～N且为整数，标号为i的球有a_i个，并保证Σa_i = M。

每次操作等概率取出一个球（即取出每个球的概率均为1/M），若这个球标号为k（k < N），则将它重新标号为k + 1；若这个球标号为N，则将其重标号为1。（取出球后并不将其丢弃）

现在你需要求出，经过K次这样的操作后，每个标号的球的期望个数。

Input

第1行包含三个正整数N，M，K，表示了标号与球的个数以及操作次数。

第2行包含N个非负整数a_i，表示初始标号为i的球有a_i个。

Output

应包含N行，第i行为标号为i的球的期望个数，四舍五入保留3位小数。

Sample Input

2 3 2
3 0

Sample Output

1.667
1.333

HINT

「样例说明」
第1次操作后，由于标号为2球个数为0，所以必然是一个标号为1的球变为标号为2的球。所以有2个标号为1的球，有1个标号为2的球。
第2次操作后，有1/3的概率标号为2的球变为标号为1的球（此时标号为1的球有3个），有2/3的概率标号为1的球变为标号为2的球（此时标号为1的球有1个），所以标号为1的球的期望个数为1/3*3+2/3*1 = 5/3。同理可求出标号为2的球期望个数为4/3。
「数据规模与约定」
对于10%的数据，N ≤ 5, M ≤ 5, K ≤ 10；
对于20%的数据，N ≤ 20, M ≤ 50, K ≤ 20；
对于30%的数据，N ≤ 100, M ≤ 100, K ≤ 100；
对于40%的数据，M ≤ 1000, K ≤ 1000；
对于100%的数据，N ≤ 1000, M ≤ 100,000,000, K ≤ 2,147,483,647。

Source

2011福建集训

题解

f(i,j)表示前i次操作，标号增加j的概率

然后枚举每个标号，计算对其它标号的期望贡献

这个dp方程很好写0.0，由于操作次数很多，所以考虑矩阵乘法，矩阵乘法是n^3logk的

观察这个矩阵，它是一个循环矩阵，两个循环矩阵乘起来还是循环矩阵，所以所有的运算过程只要保留矩阵第一行即可

这样可以优化成n^2logk

#include<map>
#include<set>
#include<cmath>
#include<cstdio>
#include<cstring>
#include<vector>
#include<iostream>
#define ll long long
using namespace std;
ll read()
{
	int x=0,f=1;char ch=getchar();
	while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
	while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
	return x*f;
}
int n,m,K;
int a[1005];
double ans[1005];
struct M{
	double v[1005];
	M(){
		memset(v,0,sizeof(v));	
	}
	friend M operator*(M a,M b){
		M c;
		for(int i=0;i<n;i++)
			for(int k=0;k<n;k++)
				c.v[i]+=a.v[(i-k+n)%n]*b.v[k];
		return c;
	}
	friend M operator^(M a,int b){
		M ans;
		ans.v[0]=1;
		for(int i=b;i;i>>=1,a=a*a)
			if(i&1)ans=ans*a;	
		return ans;
	}
}B;
int main()
{	
	n=read();m=read();K=read();
	for(int i=1;i<=n;i++)a[i]=read();	
	B.v[0]=(1.0-1.0/m);B.v[1]=1.0/m;
	M C=B^K;
	for(int i=1;i<=n;i++)
		for(int j=0;j<n;j++)
		{
			int t=i+j;
			t%=n;if(!t)t=n;
			ans[t]+=C.v[j]*a[i];
		}
	for(int i=1;i<=n;i++)
		printf("%.3lf\n",ans[i]);
	return 0;
}

#include<map>

#include<set>

#include<cmath>

#include<cstdio>

#include<cstring>

#include<vector>

#include<iostream>

#define ll long long

using namespace std;

ll read()

{

int x=0,f=1;char ch=getchar();

while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}

while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}

return x*f;

}

int n,m,K;

int a[1005];

double ans[1005];

struct M{

double v[1005];

M(){

memset(v,0,sizeof(v));

}

friend M operator*(M a,M b){

M c;

for(int i=0;i<n;i++)

for(int k=0;k<n;k++)

c.v[i]+=a.v[(i-k+n)%n]*b.v[k];

return c;

}

friend M operator^(M a,int b){

M ans;

ans.v[0]=1;

for(int i=b;i;i>>=1,a=a*a)

if(i&1)ans=ans*a;

return ans;

}

}B;

int main()

{

n=read();m=read();K=read();

for(int i=1;i<=n;i++)a[i]=read();

B.v[0]=(1.0-1.0/m);B.v[1]=1.0/m;

M C=B^K;

for(int i=1;i<=n;i++)

for(int j=0;j<n;j++)

{

int t=i+j;

t%=n;if(!t)t=n;

ans[t]+=C.v[j]*a[i];

}

for(int i=1;i<=n;i++)

printf("%.3lf\n",ans[i]);

return 0;

}

« 「BZOJ1898」Swamp 沼泽鳄鱼「泉七培训 – 郑予凡」致命漏洞 »

will7101

黄学长，最后可以直接把a矩阵乘以b矩阵，就是答案了…

Crazyxx

矩乘部分为何是a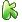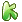 *b[j-k]，但我推出来是a 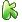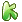*b[k-j]啊…
转移矩阵是
(m-1)/m 1/m 0 0 ….0
0 (m-1)/m 1/m 0…..0
0 0 (m-1)/m 0…..0
….

Crazyxx

想明白了TAT

cyx

为什么我有些点会出现0.0几的误差求教

hzwer

不知道我没遇到这个问题

cyx

额好吧。。。

hzwer.com _ Home | http://hzwer.com

「BZOJ2510」弱题

Description

Input

Output

Sample Input

Sample Output

HINT

Source

分类目录

热门文章

Myfriends

近期评论