「POJ3710」Christmas Game
Description
Harry and Sally were playing games at Christmas Eve. They drew some Christmas trees on a paper:
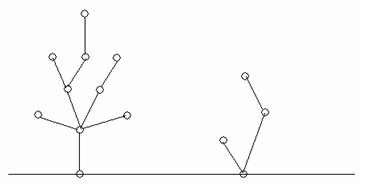
Then they took turns to cut a branch of a tree, and removed the part of the tree which had already not connected with the root. A step shows as follows:
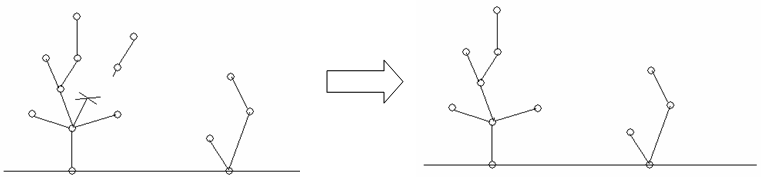
Sally always moved first. Who removed the last part of the trees would win the game.
After a while, they all figured out the best strategy and thought the game was too simple for them. Harry said, “The Christmas trees should have some gifts in them!” So Sally drew some gifts (simple polygons) in the initial trees:
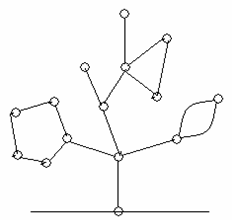
You may assume the initial picture is a tree with some simple polygons, in which each edge is involved in at most one polygon. We also know that every polygon has only one node involved in the main tree (the hanging point of the giftJ) .In every sub-tree (connected subgraph), there was one and only one node representing the “root”. According to these assumptions, following graphs will never appear:
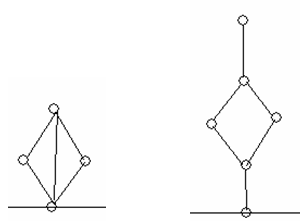
Sally and Harry took turns (Sally was always the first person to move), to cut an edge in the graph, and removed the part of the tree that no longer connected to the root. The person who cannot make a move lost the game.
Your job is to decide who will finally win the game if both of them use the best strategy.
Input
The input file contains multiply test cases.
The first line of each test case is an integer N (N<100), which represents the number of sub-trees. The following lines show the structure of the trees. The first line of the description of a tree is the number of the nodes m (m<100) and the number of the edges k (k<500). The nodes of a tree are numbered from 1 to m. Each of following lines contains 2 integers a and b representing an edge <a, b>. Node 1 is always the root.
Output
For each test case, output the name of the winner.
Sample Input
|
1 2 3 4 5 6 7 8 |
2 2 1 1 2 4 4 1 2 2 3 2 4 3 4 |
Sample Output
|
1 |
Sally |
Hint
The sample graph is
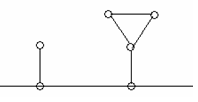
题解
树上删边游戏
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
#include<cstdio> #include<iostream> #include<cstring> #define N 1001 using namespace std; int n,m,cnt,t,to[N],next[N],head[N],w[N],s[N],top; bool vis[N],ve[N]; void insert(int u,int v) { to[++cnt]=v;next[cnt]=head[u];head[u]=cnt; to[++cnt]=u;next[cnt]=head[v];head[v]=cnt; } int dfs(int x) { vis[x]=1; int ans=0; s[++top]=x; for(int i=head[x];i;i=next[i]) if(!ve[i]) { ve[i]=1;ve[i^1]=1; int temp; if(!vis[to[i]])temp=dfs(to[i])+1; else { int q=s[top--]; while(q!=to[i]) { w[q]=1; q=s[top--]; } ++top; return 1; } if(w[to[i]])ans^=(temp)%2; else ans^=temp; } return ans; } int main() { while(scanf("%d",&t)!=EOF) { int ans=0; while(t--) { memset(head,0,sizeof(head)); memset(next,-1,sizeof(next)); memset(vis,0,sizeof(vis)); memset(ve,0,sizeof(ve)); memset(w,0,sizeof(w)); top=0;cnt=1; scanf("%d%d",&n,&m); for(int i=0;i<m;i++) { int x,y; scanf("%d%d",&x,&y); insert(x,y); } ans^=dfs(1); } if(ans)puts("Sally"); else puts("Harry"); } return 0; } |

黄学长,请问为什么不用判断环的长度的奇偶啊。QAQ
应该是有判断的吧