「CF475D」CGCDSSQ

2014年10月6日4,3800

Given a sequence of integers a₁, …, a_n and q queries x₁, …, x_q on it. For each query x_i you have to count the number of pairs (l, r)such that 1 ≤ l ≤ r ≤ n and gcd(a_l, a_l + 1, …, a_r) = x_i.

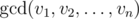$\text{[math]}$ is a greatest common divisor of v₁, v₂, …, v_n, that is equal to a largest positive integer that divides all v_i.

Input

The first line of the input contains integer n, (1 ≤ n ≤ 10⁵), denoting the length of the sequence. The next line contains n space separated integers a₁, …, a_n, (1 ≤ a_i ≤ 10⁹).

The third line of the input contains integer q, (1 ≤ q ≤ 3 × 10⁵), denoting the number of queries. Then follows q lines, each contain an integer x_i, (1 ≤ x_i ≤ 10⁹).

Output

For each query print the result in a separate line.

Sample test(s)

input

2 6 3

output

input

7
10 20 3 15 1000 60 16
10
1
2
3
4
5
6
10
20
60
1000

10 20 3 15 1000 60 16

1000

output

题解

由于gcd（a，b）=a或者<=a/2

那么枚举区间的左端点，随着右端点的推移动，区间gcd最多变化log次

那么只要通过二分找出这log个区间即可

至于区间gcd询问，可以考虑线段树或者st表，但这题线段树会多一个log是会被卡的T T

线段树（超时）

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<map>
#define ll long long 
using namespace std;
int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,q;
int a[100005],x[300005];
map<int,ll> ans;
struct data{int l,r,v;}t[400005];
int gcd(int x,int y)
{
    return y==0?x:gcd(y,x%y);
}
void build(int k,int l,int r)
{
    t[k].l=l;t[k].r=r;
    if(l==r){t[k].v=a[l];return;}
    int mid=(l+r)>>1;
    build(k<<1,l,mid);
    build(k<<1|1,mid+1,r);
    t[k].v=gcd(t[k<<1].v,t[k<<1|1].v);
}
int query(int k,int x,int y)
{
    int l=t[k].l,r=t[k].r;
    if(x==l&&y==r)return t[k].v;
    int mid=(l+r)>>1;
    if(y<=mid)return query(k<<1,x,y);
    else if(x>mid)return query(k<<1|1,x,y);
    else return gcd(query(k<<1,x,mid),query(k<<1|1,mid+1,y));
}
int find(int x,int l,int L)
{
    int r=n,ans=0;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(query(1,L,mid)!=x)r=mid-1;
        else ans=mid,l=mid+1;
    }
    return ans;
}
void solve(int x)
{
    int t=a[x],now=x;
    while(1)
    {
        int last=now;
        now=find(t,now,x);
        if(ans[t])ans[t]+=now-last+1;
        if(now==n)return;
        now++;t=query(1,x,now);
    }
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
        a[i]=read();
    build(1,1,n);
    q=read();
    for(int i=1;i<=q;i++)
        x[i]=read(),ans[x[i]]=1;
    for(int i=1;i<=n;i++)solve(i);
    for(int i=1;i<=q;i++)
        printf("%I64d\n",ans[x[i]]-1);
    return 0;
}

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstdlib>

#include<cstring>

#include<map>

#define ll long long

using namespace std;

int read()

{

int x=0,f=1;char ch=getchar();

while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}

while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}

return x*f;

}

int n,q;

int a[100005],x[300005];

map<int,ll> ans;

struct data{int l,r,v;}t[400005];

int gcd(int x,int y)

{

return y==0?x:gcd(y,x%y);

}

void build(int k,int l,int r)

{

t[k].l=l;t[k].r=r;

if(l==r){t[k].v=a[l];return;}

int mid=(l+r)>>1;

build(k<<1,l,mid);

build(k<<1|1,mid+1,r);

t[k].v=gcd(t[k<<1].v,t[k<<1|1].v);

}

int query(int k,int x,int y)

{

int l=t[k].l,r=t[k].r;

if(x==l&&y==r)return t[k].v;

int mid=(l+r)>>1;

if(y<=mid)return query(k<<1,x,y);

else if(x>mid)return query(k<<1|1,x,y);

else return gcd(query(k<<1,x,mid),query(k<<1|1,mid+1,y));

}

int find(int x,int l,int L)

{

int r=n,ans=0;

while(l<=r)

{

int mid=(l+r)>>1;

if(query(1,L,mid)!=x)r=mid-1;

else ans=mid,l=mid+1;

}

return ans;

}

void solve(int x)

{

int t=a[x],now=x;

while(1)

{

int last=now;

now=find(t,now,x);

if(ans[t])ans[t]+=now-last+1;

if(now==n)return;

now++;t=query(1,x,now);

}

int main()

{

n=read();

for(int i=1;i<=n;i++)

a[i]=read();

build(1,1,n);

q=read();

for(int i=1;i<=q;i++)

x[i]=read(),ans[x[i]]=1;

for(int i=1;i<=n;i++)solve(i);

for(int i=1;i<=q;i++)

printf("%I64d\n",ans[x[i]]-1);

return 0;

}

ST表

注意不要调用系统的log，会很慢

#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstdlib>
#include<cstring>
#include<map>
#define ll long long 
using namespace std;
int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int bin[20],Log[100005];
int n,q;
int a[100005],x[300005],f[100005][17];
map<int,ll> ans;
struct data{int l,r,v;}t[400005];
int gcd(int x,int y)
{
    return y==0?x:gcd(y,x%y);
}
void pre()
{
    for(int i=1;i<=n;i++)f[i][0]=a[i];
    for(int i=1;i<=16;i++)
        for(int x=1;x<=n;x++)
            if(x+bin[i]-1<=n)
                f[x][i]=gcd(f[x][i-1],f[x+bin[i-1]][i-1]);
            else break;
}
int query(int l,int r)
{
    int t=Log[r-l+1];
    return gcd(f[l][t],f[r-bin[t]+1][t]);
}
int find(int x,int l,int L)
{
    int r=n,ans=0;
    while(l<=r)
    {
        int mid=(l+r)>>1;
        if(query(L,mid)!=x)r=mid-1;
        else ans=mid,l=mid+1;
    }
    return ans;
}
void solve(int x)
{
    int t=a[x],now=x;
    while(1)
    {
        int last=now;
        now=find(t,now,x);
        if(ans[t])ans[t]+=now-last+1;
        if(now==n)return;
        now++;t=query(x,now);
    }
}
int main()
{
    bin[0]=1;for(int i=1;i<20;i++)bin[i]=bin[i-1]<<1;
    n=read();
    Log[0]=-1;for(int i=1;i<=n;i++)Log[i]=Log[i>>1]+1;
    for(int i=1;i<=n;i++)
        a[i]=read();
    pre();
    q=read();
    for(int i=1;i<=q;i++)
        x[i]=read(),ans[x[i]]=1;
    for(int i=1;i<=n;i++)solve(i);
    for(int i=1;i<=q;i++)
        printf("%I64d\n",ans[x[i]]-1);
    return 0;
}

#include<iostream>

#include<cstdio>

#include<cmath>

#include<cstdlib>

#include<cstring>

#include<map>

#define ll long long

using namespace std;

int read()

{

int x=0,f=1;char ch=getchar();

while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}

while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}

return x*f;

}

int bin[20],Log[100005];

int n,q;

int a[100005],x[300005],f[100005][17];

map<int,ll> ans;

struct data{int l,r,v;}t[400005];

int gcd(int x,int y)

{

return y==0?x:gcd(y,x%y);

}

void pre()

{

for(int i=1;i<=n;i++)f[i][0]=a[i];

for(int i=1;i<=16;i++)

for(int x=1;x<=n;x++)

if(x+bin[i]-1<=n)

f[x][i]=gcd(f[x][i-1],f[x+bin[i-1]][i-1]);

else break;

}

int query(int l,int r)

{

int t=Log[r-l+1];

return gcd(f[l][t],f[r-bin[t]+1][t]);

}

int find(int x,int l,int L)

{

int r=n,ans=0;

while(l<=r)

{

int mid=(l+r)>>1;

if(query(L,mid)!=x)r=mid-1;

else ans=mid,l=mid+1;

}

return ans;

}

void solve(int x)

{

int t=a[x],now=x;

while(1)

{

int last=now;

now=find(t,now,x);

if(ans[t])ans[t]+=now-last+1;

if(now==n)return;

now++;t=query(x,now);

}

int main()

{

bin[0]=1;for(int i=1;i<20;i++)bin[i]=bin[i-1]<<1;

n=read();

Log[0]=-1;for(int i=1;i<=n;i++)Log[i]=Log[i>>1]+1;

for(int i=1;i<=n;i++)

a[i]=read();

pre();

q=read();

for(int i=1;i<=q;i++)

x[i]=read(),ans[x[i]]=1;

for(int i=1;i<=n;i++)solve(i);

for(int i=1;i<=q;i++)

printf("%I64d\n",ans[x[i]]-1);

return 0;

}

« 「NOIP模拟赛」大逃亡「NOIP模拟赛」比赛 »

hzwer.com _ Home | http://hzwer.com

「CF475D」CGCDSSQ

分类目录

热门文章

Myfriends

近期评论