「BZOJ1597」[Usaco2008 Mar] 土地购买
Description
农夫John准备扩大他的农场,他正在考虑N (1 <= N <= 50,000) 块长方形的土地. 每块土地的长宽满足(1 <= 宽 <= 1,000,000; 1 <= 长 <= 1,000,000). 每块土地的价格是它的面积,但FJ可以同时购买多快土地. 这些土地的价格是它们最大的长乘以它们最大的宽, 但是土地的长宽不能交换. 如果FJ买一块3×5的地和一块5×3的地,则他需要付5×5=25. FJ希望买下所有的土地,但是他发现分组来买这些土地可以节省经费. 他需要你帮助他找到最小的经费.
Input
* 第1行: 一个数: N
* 第2..N+1行: 第i+1行包含两个数,分别为第i块土地的长和宽
Output
* 第一行: 最小的可行费用.
Sample Input
4
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.
100 1
15 15
20 5
1 100
输入解释:
共有4块土地.
Sample Output
500
HINT
FJ分3组买这些土地: 第一组:100×1, 第二组1×100, 第三组20×5 和 15×15 plot. 每组的价格分别为100,100,300, 总共500.
题解
妈蛋被各种题解坑了半天不如自己手推靠谱
按照x，y递增排序，然后把可以和其它打包一起买的去掉
然后使得剩下一些y递减x递增的矩形
显然f[i]=min(f[j]+y[j+1]x[i])
然后再搞个斜率优化
方程是(f[j]-f[k])/(y[k+1]-y[j+1])<x[i]
然后维护一个下凸包
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 |
#include<iostream> #include<cstdio> #include<algorithm> #define ll long long using namespace std; inline int read() { int x=0;char ch=getchar(); while(ch<'0'||ch>'9')ch=getchar(); while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x; } int n,tot; ll x[50005],y[50005],f[50005];; int q[50005]; struct data{ll x,y;}a[50005]; inline bool cmp(data a,data b) {return a.x==b.x?a.y<b.y:a.x<b.x;} inline double slop(int a,int b) {return (double)(f[b]-f[a])/(y[a+1]-y[b+1]);} int main() { n=read(); for(int i=1;i<=n;i++) a[i].x=read(),a[i].y=read(); sort(a+1,a+n+1,cmp); for(int i=1;i<=n;i++) { while(tot&&a[i].y>=y[tot])tot--; x[++tot]=a[i].x;y[tot]=a[i].y; } int l=0,r=0; for(int i=1;i<=tot;i++) { while(l<r&&slop(q[l],q[l+1])<x[i])l++; int t=q[l]; f[i]=f[t]+y[t+1]*x[i]; while(l<r&&slop(q[r],i)<slop(q[r-1],q[r]))r--; q[++r]=i; } printf("%lld",f[tot]); return 0; } |
计数器 9787808
OI 课件=>
OI 课件=>
应该是大于的。。。。
“然后再搞个斜率优化
方程是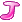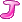(f
-f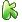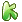 
)/(y[k+1]-y[j+1])<x 
”
应该是大于吧？