数学 - Page 17 - hzwer.com

「BZOJ1188」[HNOI2007] 分裂游戏
Description聪聪和睿睿最近迷上了一款叫做分裂的游戏。该游戏的规则试：共有n个瓶子，标号为0,1,2.....n-1,第i个瓶子中装有p[i]颗巧克力豆，两个人轮流取豆子，每一轮每人选择3个瓶子。标号为i,j,k,并要保证i<j,j<=k且第i个瓶子中至少要有1颗巧克力豆，随后这个人从第i个瓶子中拿走一颗豆子并在j,k中各放入一粒豆子（j可能等于k）。如果轮到某人而他无法按规则取豆子，那么他将输掉比赛。胜利者可以拿走所有的巧克力豆！两人...
12014年3月12日5,135博弈论

「POJ3710」Christmas Game
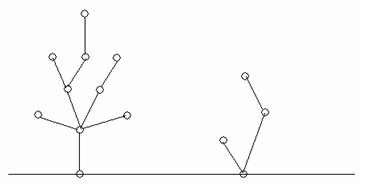
DescriptionHarryandSallywereplayinggamesatChristmasEve.TheydrewsomeChristmastreesonapaper:Thentheytookturnstocutabranchofatree,andremovedthepartofthetreewhichhadalreadynotconnectedwiththeroot.Astepshowsasfollows:Sallyalwaysmovedfirst.Whoremovedthelastpartofthetreeswouldwinthegame.Afterawhile,theyallfiguredoutthebeststrategyandthoughtthegamewastoosimpleforthem.Harrysaid,“TheChristma...
22014年3月12日4,816博弈论
「POJ3480」John
DescriptionLittleJohnisplayingveryfunnygamewithhisyoungerbrother.ThereisonebigboxfilledwithM&Msofdifferentcolors.AtfirstJohnhastoeatseveralM&Msofthesamecolor.Thenhisopponenthastomakeaturn.Andsoon.PleasenotethateachplayerhastoeatatleastoneM&Mduringhisturn.IfJohn(orhisbrother)willeatthelastM&Mfromtheboxhewillbeconsideredasalooserandhewillhavetobuyanewcandybox.Both...
02014年3月11日4,078博弈论
「POJ2068」Nim
DescriptionLet'splayatraditionalgameNim.YouandIareseatedacrossatableandwehaveahundredstonesonthetable(weknowthenumberofstonesexactly).Weplayinturnandateachturn,youorIcanremoveontofourstonesfromtheheap.Youplayfirstandtheonewhoremovedthelaststoneloses.Inthisgame,youhaveawinningstrategy.Toseethis,youfirstremovefourstonesandleave96stones.NomatterhowIplay,Iwillendupwithleaving92-95stones.T...
02014年3月11日3,472博弈论,记忆化搜索
「POJ2960」S – Nim
DescriptionArthurandhissisterCarollhavebeenplayingagamecalledNimforsometimenow.Nimisplayedasfollows:Thestartingpositionhasanumberofheaps,allcontainingsome,notnecessarilyequal,numberofbeads.Theplayerstaketurnschosingaheapandremovingapositivenumberofbeadsfromit.Thefirstplayernotabletomakeamove,loses.ArthurandCarollreallyenjoyedplayingthissimplegameuntiltheyrecentlylearnedaneasywaytoalwaysb...
02014年3月11日4,387博弈论
「BZOJ1227」[SDOI2009] 虔诚的墓主人
题目描述 Description小W是一片新造公墓的管理人。公墓可以看成一块N×M的矩形，矩形的每个格点，要么种着一棵常青树，要么是一块还没有归属的墓地。当地的居民都是非常虔诚的基督徒，他们愿意提前为自己找一块合适墓地。为了体现自己对主的真诚，他们希望自己的墓地拥有着较高的虔诚度。一块墓地的虔诚度是指以这块墓地为中心的十字架的数目。一个十字架可以看成中间是墓地，墓地的正上、正下、正左、正右都有恰好k棵常青树。...
42014年3月11日6,851树状数组,排列组合
「POJ2484」A Funny Game
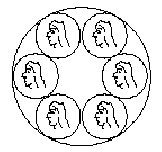
DescriptionAliceandBobdecidetoplayafunnygame.Atthebeginningofthegametheypickn(1<=n<=106)coinsinacircle,asFigure1shows.Amoveconsistsinremovingoneortwoadjacentcoins,leavingallothercoinsuntouched.Atleastonecoinmustberemoved.PlayersalternatemoveswithAlicestarting.Theplayerthatremovesthelastcoinwins.(Thelastplayertomovewins.Ifyoucan'tmove,youlose.)Figure1Note:Forn>3,weusec1,c2,....
02014年3月10日2,919博弈论
「POJ2505」A multiplication game
DescriptionStanandOllieplaythegameofmultiplicationbymultiplyinganintegerpbyoneofthenumbers2to9.Stanalwaysstartswithp=1,doeshismultiplication,thenOlliemultipliesthenumber,thenStanandsoon.Beforeagamestarts,theydrawaninteger1<n<4294967295andthewinneriswhofirstreachesp>=n.InputEachlineofinputcontainsoneintegernumbern.OutputForeachlineofinputoutputonelineeitherStanwins.orOlliewins...
02014年3月10日3,765博弈论
「POJ2425」A Chess Game
DescriptionLet'sdesignanewchessgame.ThereareNpositionstoholdMchessesinthisgame.Multiplechessescanbelocatedinthesameposition.Thepositionsareconstitutedasatopologicalgraph,i.e.therearedirectededgesconnectingsomepositions,andnocycleexists.TwoplayersyouandImovechessesalternately.Ineachturntheplayershouldmoveonlyonechessfromthecurrentpositiontooneofitsout-positionsalonganedge.Thegamedoesnote...
02014年3月10日2,770博弈论
「POJ2975」Nim
DescriptionNimisa2-playergamefeaturingseveralpilesofstones.Playersalternateturns,andonhis/herturn,aplayer’smoveconsistsofremoving oneormorestones fromanysinglepile.Playendswhenallthestoneshavebeenremoved,atwhichpointthelastplayertohavemovedisdeclaredthewinner.GivenapositioninNim,yourtaskistodeterminehowmanywinningmovesthereareinthatposition.ApositioninNimiscalled“losing”ifthefirstplay...
02014年3月9日3,013博弈论
「CF400C」Inna and Huge Candy Matrix
InnaandDimadecidedtosurpriseSereja.Theybroughtareallyhugecandymatrix,it'sbigevenforSereja!Let'snumbertherowsofthegiantmatrixfrom 1 to n fromtoptobottomandthecolumns—from 1 to m,fromlefttoright.We'llrepresentthecellontheintersectionofthe i-throwand j-thcolumnas (i, j).Justasisexpected,somecellsofthegiantcandymatrixcontaincandies.Overallthematrixhas p candies:the k-thcandyisa...
02014年3月6日2,733矩阵乘法
「POJ3150」Cellular Automaton
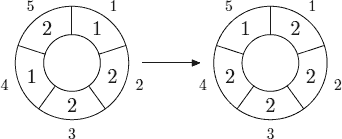
DescriptionA cellularautomaton isacollectionofcellsonagridofspecifiedshapethatevolvesthroughanumberofdiscretetimestepsaccordingtoasetofrulesthatdescribethenewstateofacellbasedonthestatesofneighboringcells.The orderofthecellularautomaton isthenumberofcellsitcontains.Cellsoftheautomatonoforder n arenumberedfrom1to n.The orderofthecell isthenumberofdifferentvaluesitmaycontain.Usually,v...
02014年3月4日4,146递推与动规,矩阵乘法