「POJ2187」Beauty Contest

2015年1月25日8,1371

Description

Bessie, Farmer John’s prize cow, has just won first place in a bovine beauty contest, earning the title ‘Miss Cow World’. As a result, Bessie will make a tour of N (2 <= N <= 50,000) farms around the world in order to spread goodwill between farmers and their cows. For simplicity, the world will be represented as a two-dimensional plane, where each farm is located at a pair of integer coordinates (x,y), each having a value in the range -10,000 … 10,000. No two farms share the same pair of coordinates.Even though Bessie travels directly in a straight line between pairs of farms, the distance between some farms can be quite large, so she wants to bring a suitcase full of hay with her so she has enough food to eat on each leg of her journey. Since Bessie refills her suitcase at every farm she visits, she wants to determine the maximum possible distance she might need to travel so she knows the size of suitcase she must bring.Help Bessie by computing the maximum distance among all pairs of farms.

Input

* Line 1: A single integer, N* Lines 2..N+1: Two space-separated integers x and y specifying coordinate of each farm

Output

* Line 1: A single integer that is the squared distance between the pair of farms that are farthest apart from each other.

Sample Input

0 0

0 1

1 1

1 0

Sample Output

2

Hint

Farm 1 (0, 0) and farm 3 (1, 1) have the longest distance (square root of 2)

题解

旋转卡壳

旋转(zhuan4)卡（qia3）壳（ke2）是这么念的么2333

网上似乎教程都是这样：

旋转卡壳可以用于求凸包的直径、宽度，两个不相交凸包间的最大距离和最小距离等。虽然算法的思想不难理解，但是实现起来真的很容易让人“卡壳”。
拿凸包直径(也就是凸包上最远的两点的距离）为例，原始的算法是这样子：

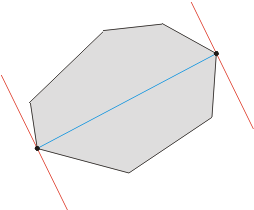
Compute the polygon’s extreme points in the y direction. Call them ymin and ymax.
Construct two horizontal lines of support through ymin and ymax. Since this is already an anti-podal pair, compute the distance, and keep as maximum.
Rotate the lines until one is flush with an edge of the polygon.
A new anti-podal pair is determined. Compute the new distance, compare to old maximum, and update if necessary.
Repeat steps 3 and 4 until the anti-podal pair considered is (ymin,ymax) again.
Output the pair(s) determining the maximum as the diameter pair(s).

更具体的可参见http://cgm.cs.mcgill.ca/~orm/rotcal.frame.html

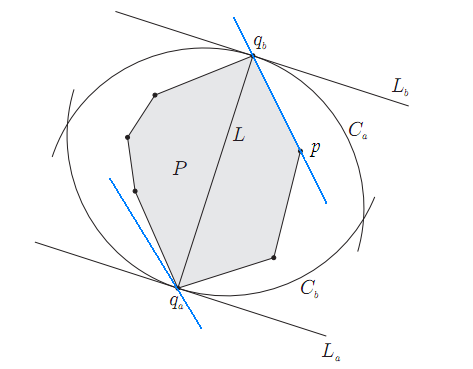
直接按照这个描述可以实现旋转卡壳算法，但是代码肯定相当冗长。逆向思考，如果q_a，q_b是凸包上最远两点，必然可以分别过q_a，q_b画出一对平行线。通过旋转这对平行线，我们可以让它和凸包上的一条边重合,如图中蓝色直线，可以注意到，q_a是凸包上离p和q_b所在直线最远的点。于是我们的思路就是枚举凸包上的所有边，对每一条边找出凸包上离该边最远的顶点，计算这个顶点到该边两个端点的距离，并记录最大的值。直观上这是一个O(n²)的算法，和直接枚举任意两个顶点一样了。但是注意到当我们逆时针枚举边的时候，最远点的变化也是逆时针的，这样就可以不用从头计算最远点，而可以紧接着上一次的最远点继续计算(详细的证明可以参见上面链接中的论文)。于是我们得到了O(n)的算法。

其实直接看代码就好了T T

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cstdlib>
#include<set>
#include<ctime>
#include<vector>
#include<queue>
#include<algorithm>
#include<map>
#include<cmath>
#define eps 1e-8
#define inf 1000000000
#define pa pair<int,int>
#define ll long long 
using namespace std;
int read()
{
    int x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n,top;
double ans;
double sqr(double x)
{

	return x*x;
}
struct P{
	double x,y;
	P(){}
	P(double _x,double _y):x(_x),y(_y){}
	friend P operator +(P a,P b){
		return P(a.x+b.x,a.y+b.y);
	}
	friend P operator -(P a,P b){
		return P(a.x-b.x,a.y-b.y);
	}
	friend double operator*(P a,P b){
		return a.x*b.y-a.y*b.x;
	}
	friend double operator/(P a,P b){
		return a.x*b.x+a.y*b.y;
	}
	friend bool operator==(P a,P b){
		return fabs(a.x-b.x)<eps&&fabs(a.y-b.y)<eps;
	}
	friend bool operator!=(P a,P b){
		return !(a==b);
	}
	friend bool operator<(P a,P b){
		if(fabs(a.y-b.y)<eps)return a.x<b.x;
		return a.y<b.y;
	}
	friend double dis2(P a){
		return sqr(a.x)+sqr(a.y);
	}
	friend void print(P a){
		printf("%.2lf %.2lf\n",a.x,a.y);
	}
}p[50005],q[50005];
bool cmp(P a,P b)
{
	if(fabs((b-p[1])*(a-p[1]))<eps)return dis2(a-p[1])<dis2(b-p[1]);
	return (a-p[1])*(b-p[1])>0;
}
void graham()
{
	for(int i=1;i<=n;i++)
		if(p[i]<p[1])swap(p[i],p[1]);
	sort(p+2,p+n+1,cmp);
	q[++top]=p[1];q[++top]=p[2];
	for(int i=3;i<=n;i++)
	{
		while((q[top]-q[top-1])*(p[i]-q[top-1])<eps&&top>1)top--;
		q[++top]=p[i];
	}
}
void RC()
{
	q[top+1]=q[1];
	int now=2;
	for(int i=1;i<=top;i++)
	{
		while((q[i+1]-q[i])*(q[now]-q[i])<(q[i+1]-q[i])*(q[now+1]-q[i]))
		{
			now++;
			if(now==top+1)now=1;
		}
		ans=max(ans,dis2(q[now]-q[i]));
	}
}
int main()
{
	n=read();
	for(int i=1;i<=n;i++)
		p[i].x=read(),p[i].y=read();
	graham();
	RC();
	printf("%d",(int)ans);
	return 0;
}

100

101

102

103

104

#include<iostream>

#include<cstdio>

#include<cstring>

#include<cstdlib>

#include<set>

#include<ctime>

#include<vector>

#include<queue>

#include<algorithm>

#include<map>

#include<cmath>

#define eps 1e-8

#define inf 1000000000

#define pa pair<int,int>

#define ll long long

using namespace std;

int read()

{

int x=0,f=1;char ch=getchar();

while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}

while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}

return x*f;

}

int n,top;

double ans;

double sqr(double x)

{

return x*x;

}

struct P{

double x,y;

P(){}

P(double _x,double _y):x(_x),y(_y){}

friend P operator +(P a,P b){

return P(a.x+b.x,a.y+b.y);

}

friend P operator -(P a,P b){

return P(a.x-b.x,a.y-b.y);

}

friend double operator*(P a,P b){

return a.x*b.y-a.y*b.x;

}

friend double operator/(P a,P b){

return a.x*b.x+a.y*b.y;

}

friend bool operator==(P a,P b){

return fabs(a.x-b.x)<eps&&fabs(a.y-b.y)<eps;

}

friend bool operator!=(P a,P b){

return !(a==b);

}

friend bool operator<(P a,P b){

if(fabs(a.y-b.y)<eps)return a.x<b.x;

return a.y<b.y;

}

friend double dis2(P a){

return sqr(a.x)+sqr(a.y);

}

friend void print(P a){

printf("%.2lf %.2lf\n",a.x,a.y);

}

}p[50005],q[50005];

bool cmp(P a,P b)

{

if(fabs((b-p[1])*(a-p[1]))<eps)return dis2(a-p[1])<dis2(b-p[1]);

return (a-p[1])*(b-p[1])>0;

}

void graham()

{

for(int i=1;i<=n;i++)

if(p[i]<p[1])swap(p[i],p[1]);

sort(p+2,p+n+1,cmp);

q[++top]=p[1];q[++top]=p[2];

for(int i=3;i<=n;i++)

{

while((q[top]-q[top-1])*(p[i]-q[top-1])<eps&&top>1)top--;

q[++top]=p[i];

}

void RC()

{

q[top+1]=q[1];

int now=2;

for(int i=1;i<=top;i++)

{

while((q[i+1]-q[i])*(q[now]-q[i])<(q[i+1]-q[i])*(q[now+1]-q[i]))

{

now++;

if(now==top+1)now=1;

}

ans=max(ans,dis2(q[now]-q[i]));

}

int main()

{

n=read();

for(int i=1;i<=n;i++)

p[i].x=read(),p[i].y=read();

graham();

RC();

printf("%d",(int)ans);

return 0;

}

« 「BZOJ1185」[HNOI2007] 最小矩形覆盖「BZOJ2829」信用卡凸包 »

咸鱼

这个实现方式值得借鉴呀

hzwer.com _ Home | http://hzwer.com

「POJ2187」Beauty Contest

分类目录

热门文章

Myfriends

近期评论