「CF403C」Strictly Positive Matrix
来自zld神犇的题解
学过矩阵的人都知道对于本题来说整个矩阵里的元素只需要分为两种,一种是为0,一种是不为0。
这样我们就得到了一个01矩阵= =
我们看看这题的标签= =
卧槽。。这TM跟图论有什么关系。。
对邻接矩阵比较熟悉的的人没看到这个标签也可能一下子就能想到怎么回事,该矩阵表示对应的有向图,第i行第j列表示第i个点能否直接走到第j个点,而这个矩阵的k次幂中,第i行第j列表示第i个点走恰好k步能否走到第j个点。
于是我们就把这道题转到图论上去了。。由邻接矩阵幂的性质我们猜想当且仅当这个矩阵代表的有向图为强连通图的时候答案为YES。
证明:
当这个矩阵(01矩阵,边权为1)代表的有向图为强连通图的时候,设有自环的那个点为mid,取(U,V)两点使得U–>mid–>V最短路径的长度最大,记为k。
那么我们考虑任意一对(u,v),我们构造一条u–>mid–>v的最短路径,如果这条路径的长度<k,那么我们走mid的自环直到长度补齐为止,而>k显然是不可能的,这个时候我们就找到了这样的正整数k,使得该矩阵的k次幂中每一项全部为正数,此时答案为YES。
(利用上面一段证明我们可以如果k存在那么其上界为2n,因此50分做法只需要取一个矩阵的2n次幂判断即可。)
当这个矩阵代表的不是强连通图,取(u,v)使u始终不能到达v,无论取几次幂,该矩阵中第u行第v列始终为0,此时答案为NO。
直接BFS的时间复杂度为n^3,而用Tarjan算法的话时间复杂度为n^2。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 |
#include<iostream> #include<cstdio> #include<cstring> #include<cstdlib> #include<set> #include<ctime> #include<vector> #include<queue> #include<algorithm> #include<map> #include<cmath> #define eps 1e-8 #define inf 1000000000 #define pa pair<int,int> #define ll long long using namespace std; int read() { int x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int T,n,cnt,ind,scc,top; int last[2005],dfn[2005],low[2005],q[2005]; bool inq[2005]; struct edge{ int to,next; }e[4000005]; void insert(int u,int v) { e[++cnt].to=v;e[cnt].next=last[u];last[u]=cnt; } void tarjan(int x) { dfn[x]=low[x]=++ind; q[++top]=x;inq[x]=1; for(int i=last[x];i;i=e[i].next) if(!dfn[e[i].to]) tarjan(e[i].to),low[x]=min(low[x],low[e[i].to]); else if(inq[e[i].to]) low[x]=min(low[x],dfn[e[i].to]); int now=-1; if(low[x]==dfn[x]) { scc++; while(now!=x) { now=q[top--]; inq[now]=0; } } } int main() { n=read(); for(int i=1;i<=n;i++) for(int j=1;j<=n;j++) { int x=read(); if(x)insert(i,j); } for(int i=1;i<=n;i++) if(!dfn[i])tarjan(i); if(scc==1)puts("YES"); else puts("NO"); return 0; } |
Subscribe

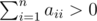 .
.