「CF477B」Dreamoon and Sets

2014年10月13日3,9230

Dreamoon likes to play with sets, integers and 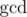. 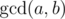is defined as the largest positive integer that divides both a and b.

Let S be a set of exactly four distinct integers greater than 0. Define S to be of rank k if and only if for all pairs of distinct elements si, sj from S, .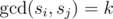

Given k and n, Dreamoon wants to make up n sets of rank k using integers from 1 to msuch that no integer is used in two different sets (of course you can leave some integers without use). Calculate the minimum m that makes it possible and print one possible solution.

Input

The single line of the input contains two space separated integers n, k (1 ≤ n ≤ 10 000, 1 ≤ k ≤ 100).

Output

On the first line print a single integer — the minimal possible m.

On each of the next n lines print four space separated integers representing the i-th set.

Neither the order of the sets nor the order of integers within a set is important. If there are multiple possible solutions with minimal m, print any one of them.

Sample test(s)
input

output

input

output

Note

For the first example it’s easy to see that set {1, 2, 3, 4} isn’t a valid set of rank 1 since .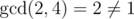

题解

本质就是求n个集合，元素互不相同，每个集合4个互质的数，要求最大值最小

公约数k即所有元素都乘上k即可

每个集合显然只能有一个偶数，而且发现每三个奇数都是互质的。。。

然后偶数也要跟这些奇数互质。。

那么只要

2 1 3 5

8 7 9 11

14 13 15 17

这样构造就可以了

 

avatar
  Subscribe  
提醒