「fjWC2015」k个串 kstring
「题目描述」
兔子们在玩k个串的游戏。首先,它们拿出了一个长度为n的数字序列,选出其中的一个连续子串,然后统计其子串中所有数字之和(注意这里重复出现的数字只被统计一次)。
兔子们想知道,在这个数字序列所有连续的子串中,按照以上方式统计其所有数字之和,第k大的和是多少。
「输入格式」
第一行,两个整数n和k,分别表示长度为n的数字序列和想要统计的第k大的和
接下里一行n个数a_i,表示这个数字序列
「输出格式」
一行一个整数,表示第k大的和
「样例输入」
7 5
3 -2 1 2 2 1 3 -2
「样例输出」
4
「数据范围」
对于20%的数据,1 <= n <= 2000
对于另外20%的数据,0 <= a_i <= 10^9
对于100%的数据,1 <= n <= 100000, 1 <= k <= 200000, 0 <= |a_i| <= 10^9
数据保证存在第k大的和
题解
我竟然写了个40分T T
前20的暴力随便map+sort水过
对于全是正数的情况,若固定右端点,则左端点等于1时一定最大
将1- i (1<=i<=n) 的值放入堆
每次从堆中取出最大值,若其区间为 l ~ r ,加入 l+1 ~ r,重复此操作K次
查询一个区间不重复值的权值和,只要记录每个数下次出现的位置nxt[x],然后将nxt[x]和v[x]放进主席树里就可以解决了
复杂度n(logn)^2
40分
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 |
#include<set> #include<map> #include<cmath> #include<ctime> #include<queue> #include<cstdio> #include<vector> #include<cstring> #include<cstdlib> #include<iostream> #include<algorithm> #define rad 100000000 #define inf 1000000000 #define ll long long #define eps 1e-10 #define pi acos(-1) #define mod 10000 using namespace std; ll read() { ll x=0,f=1;char ch=getchar(); while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();} while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();} return x*f; } int n,K,cnt; int a[100005],root[100005],nxt[100005]; int ls[10000005],rs[10000005],sum[10000005]; struct data{ int val,l,r; }; bool operator<(data a,data b) { return a.val<b.val; } priority_queue<data,vector<data> >q; map<int,int> mp; void insert(int x,int &y,int l,int r,int pos,int val) { y=++cnt; if(l==r){sum[y]=sum[x]+val;return;} ls[y]=ls[x];rs[y]=rs[x]; int mid=(l+r)>>1; if(pos<=mid) insert(ls[x],ls[y],l,mid,pos,val); else insert(rs[x],rs[y],mid+1,r,pos,val); sum[y]=sum[ls[y]]+sum[rs[y]]; } int query(int p1,int p2,int l,int r,int val) { if(l==r)return 0; int mid=(l+r)>>1; if(val<=mid)return sum[rs[p2]]-sum[rs[p1]]+query(ls[p1],ls[p2],l,mid,val); else return query(rs[p1],rs[p2],mid+1,r,val); } int query(int x,int y) { return query(root[x-1],root[y],1,n+1,y); } vector<int> ve; void add(int l) { mp.clear(); int tot=0; for(int i=l;i<=n;i++) { if(!mp[a[i]])mp[a[i]]=1,tot+=a[i]; ve.push_back(tot); } } void solve1() { for(int l=1;l<=n;l++) add(l); sort(ve.begin(),ve.end(),greater<int>()); printf("%d",ve[K-1]); } int main() { n=read();K=read(); for(int i=1;i<=n;i++)a[i]=read(); if(n<=2000) { solve1(); return 0; } for(int i=n;i;i--) { nxt[i]=mp[a[i]]; if(!nxt[i])nxt[i]=n+1; mp[a[i]]=i; } for(int i=1;i<=n;i++) insert(root[i-1],root[i],1,n+1,nxt[i],a[i]); for(int i=1;i<=n;i++) q.push((data){query(1,i),1,i}); int ans; for(int i=1;i<=K;i++) { data t=q.top();q.pop(); ans=t.val; if(t.l<t.r)q.push((data){query(t.l+1,t.r),t.l+1,t.r}); } printf("%d\n",ans); return 0; } |

求这题标算>_<
我们对于每个位置i,维护以它为左端点的所有子串的和(注意这里的和均为重复的数字只统计一次),并令c 为其为左端点的子串和的最大值。
为其为左端点的子串和的最大值。 的最大值,不妨设为是c
的最大值,不妨设为是c 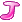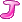 ,这时我们用j为左端点的所有子串中的次大值来更新c
,这时我们用j为左端点的所有子串中的次大值来更新c 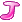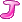 。
。 。首先,我们令b
。首先,我们令b  为[1, i]之间所有和,并以b
为[1, i]之间所有和,并以b  建立一棵线段树T。然后,我们发现,以2为右端点的子串所构成的线段树,就是T将[2, next
建立一棵线段树T。然后,我们发现,以2为右端点的子串所构成的线段树,就是T将[2, next  )区间内所有数减a
)区间内所有数减a  (next
(next  表示a
表示a  在i之后下一次出现的位置),T中1位置赋为-inf的线段树,同理3,4…n为左端点的线段树,都可以由上一个修改而来。
在i之后下一次出现的位置),T中1位置赋为-inf的线段树,同理3,4…n为左端点的线段树,都可以由上一个修改而来。 的最大值,使用一个堆来维护就可以了。
的最大值,使用一个堆来维护就可以了。
对于全局最大的和,显然它是所有c
以上过程重复k次即可找出k大值。
下面考虑如何维护c
于是,可以使用可持久化线段树来维护他们,同时,删除最大值和查询最大值也可轻松实现。而所有c
总的时间复杂度为O((n+k)lgn)
感觉不对啊,为什么重复那个操作K次就能找到K大值呢?第j-1个数如果是-1那么次大值不应该是以j-1为左端点的子串和么?= =
这是包括负数的情况吧?b[i]建树是以位置建树还是权值建树?