博弈论 - Page 2

「FJOI2013」圆形游戏
题目描述在一个无穷大的桌面上有n个圆形，保证任意2个圆相离或者相含，不存在相切或相交。现在Alice和Bob在玩一个圆形游戏，以Alice为先手，双方以如下步骤轮流游戏：1) 选定一个圆A，把A以及所有完全在A内部的圆都删除；2) 如果在自己回合无法找到可删除的圆，则输掉比赛。假设Alice和Bob都非常聪明，请问最终谁能够取得胜利？请编程输出最终获胜的人。输入输入数据的第一行为一个正整数T，表示数据组数。接下来T组数...
42014年9月23日5,062几何,博弈论

「NOIP模拟赛」环上的游戏
环上的游戏（cycle）有一个取数的游戏。初始时，给出一个环，环上的每条边上都有一个非负整数。这些整数中至少有一个0。然后，将一枚硬币放在环上的一个节点上。两个玩家就是以这个放硬币的节点为起点开始这个游戏，两人轮流取数，取数的规则如下：（1）选择硬币左边或者右边的一条边，并且边上的数非0；（2）将这条边上的数减至任意一个非负整数(至少要有所减小)；（3）将硬币移至边的另一端。如果轮到一个玩家走，这时硬币左右两...
02014年9月13日2,876博弈论
「CF451A」Game With Sticks
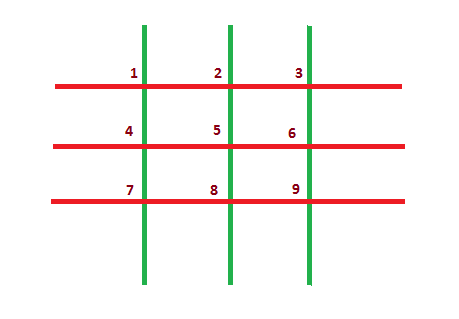
AfterwinninggoldandsilverinIOI2014,AkshatandMalvikawanttohavesomefun.Nowtheyareplayingagameonagridmadeof nhorizontaland m verticalsticks.An intersectionpoint isanypointonthegridwhichisformedbytheintersectionofonehorizontalstickandoneverticalstick.Inthegridshownbelow, n = 3 and m = 3.Thereare n + m = 6 sticksintotal(horizontalsticksareshowninredandverticalsticksareshowni...
02014年7月25日3,169博弈论
「BZOJ1115」[POI2009] 石子游戏Kam
Description有N堆石子，除了第一堆外，每堆石子个数都不少于前一堆的石子个数。两人轮流操作每次操作可以从一堆石子中移走任意多石子，但是要保证操作后仍然满足初始时的条件谁没有石子可移时输掉游戏。问先手是否必胜。Input第一行u表示数据组数。对于每组数据，第一行N表示石子堆数，第二行N个数ai表示第i堆石子的个数(a1<=a2<=……<=an)。1<=u<=101<=n<=10000<=ai<=10000Outputu行，若先手必胜...
02014年5月13日4,022博弈论
「BZOJ1874」[BJ2009 WinterCamp] 取石子游戏
Description小H和小Z正在玩一个取石子游戏。取石子游戏的规则是这样的，每个人每次可以从一堆石子中取出若干个石子，每次取石子的个数有限制，谁不能取石子时就会输掉游戏。小H先进行操作，他想问你他是否有必胜策略，如果有，第一步如何取石子。Input输入文件的第一行为石子的堆数N接下来N行，每行一个数Ai，表示每堆石子的个数接下来一行为每次取石子个数的种类数M接下来M行，每行一个数Bi，表示每次可以取的石子个数...
02014年4月21日4,420博弈论
「BZOJ2463」[中山市选2009] 谁能赢呢？
Description小明和小红经常玩一个博弈游戏。给定一个n×n的棋盘，一个石头被放在棋盘的左上角。他们轮流移动石头。每一回合，选手只能把石头向上，下，左，右四个方向移动一格，并且要求移动到的格子之前不能被访问过。谁不能移动石头了就算输。假如小明先移动石头，而且两个选手都以最优策略走步，问最后谁能赢？Input 输入文件有多组数据。输入第一行包含一个整数n，表示棋盘的规模。当输入n为0时，表示...
02014年4月15日4,420博弈论
「th04」秋静叶&秋穣子
Description在幻想乡，秋姐妹是掌管秋天的神明，作为红叶之神的姐姐静叶和作为丰收之神的妹妹穰子。如果把红叶和果实联系在一起，自然会想到烤红薯。烤红薯需要很多的叶子，才能把红薯烤得很香，所以秋姐妹决定比比谁能够收集到最多的红叶。静叶将红叶分成了N堆(编号1..N)，并且规定了它们的选取顺序，刚好形成一颗有向树。在游戏过程中，两人从根节点开始，轮流取走红叶，当一个人取走节点i的红叶后，另一个人只能从节点i的儿子...
02014年3月23日3,549树形动规,博弈论
「BZOJ1982」[SPOJ 2021] Moving Pebbles
Description2021.MovingPebblesTwoplayersplaythefollowinggame.Atthebeginningofthegametheystartwithn(1<=n<=100000)pilesofstones.Ateachstepofthegame,theplayerchoosesapileandremoveatleastonestonefromthispileandmovezeroormorestonesfromthispiletoanyotherpilethatstillhasstones.Aplayerlosesifhehasnomorepossiblemoves.Giventheinitialpiles,determinewhowins:thefirstplayer,orthesecondplayer,ifboth...
02014年3月22日4,043博弈论
「BZOJ1299」[LLH邀请赛] 巧克力棒
DescriptionTBL和X用巧克力棒玩游戏。每次一人可以从盒子里取出若干条巧克力棒，或是将一根取出的巧克力棒吃掉正整数长度。TBL先手两人轮流，无法操作的人输。他们以最佳策略一共进行了10轮（每次一盒）。你能预测胜负吗？Input输入数据共20行。第2i-1行一个正整数Ni，表示第i轮巧克力棒的数目。第2i行Ni个正整数Li,j，表示第i轮巧克力棒的长度。Output输出数据共10行。每行输出“YES”或“NO”，表示TBL是否...
02014年3月13日5,460博弈论
「POJ3537」Crosses and Crosses
DescriptionThegameof CrossesandCrosses isplayedonthefieldof1× n cells.Twoplayersmakemovesinturn.Eachmovetheplayerselectsanyfreecellonthefieldandputsacross‘×’toit.Ifaftertheplayer’smovetherearethreecrossesinarow,hewins.Youaregiven n.Findoutwhowinsifbothplayersplayoptimally.InputInputfilecontainsoneintegernumber n (3≤ n ≤2000).OutputOutput‘1’ifthefirstplayerwins,or‘2’...
02014年3月13日3,129博弈论
「BZOJ1188」[HNOI2007] 分裂游戏
Description聪聪和睿睿最近迷上了一款叫做分裂的游戏。该游戏的规则试：共有n个瓶子，标号为0,1,2.....n-1,第i个瓶子中装有p[i]颗巧克力豆，两个人轮流取豆子，每一轮每人选择3个瓶子。标号为i,j,k,并要保证i<j,j<=k且第i个瓶子中至少要有1颗巧克力豆，随后这个人从第i个瓶子中拿走一颗豆子并在j,k中各放入一粒豆子（j可能等于k）。如果轮到某人而他无法按规则取豆子，那么他将输掉比赛。胜利者可以拿走所有的巧克力豆！两人...
12014年3月12日5,132博弈论
「POJ3710」Christmas Game
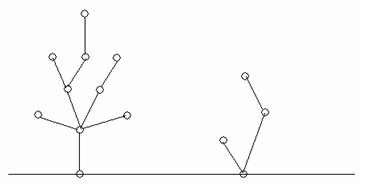
DescriptionHarryandSallywereplayinggamesatChristmasEve.TheydrewsomeChristmastreesonapaper:Thentheytookturnstocutabranchofatree,andremovedthepartofthetreewhichhadalreadynotconnectedwiththeroot.Astepshowsasfollows:Sallyalwaysmovedfirst.Whoremovedthelastpartofthetreeswouldwinthegame.Afterawhile,theyallfiguredoutthebeststrategyandthoughtthegamewastoosimpleforthem.Harrysaid,“TheChristma...
22014年3月12日4,813博弈论